Contents
Ejercicio 1
Imprimir una tabla formateada (entero y real) del logaritmo natural de los números 10, 20, 40, 60, y 80. Sugerencia: usar el comando fprintf y vectores
x=[10; 20; 40; 60; 80]; y=[x, log(x)]; fprintf('\n Numero Natural log\n') fprintf('%4i \t %8.3f\n',y')
Numero Natural log 10 2.303 20 2.996 40 3.689 60 4.094 80 4.382
Ejercicio 2
Hallar el vector X para la siguiente ecuación matricial:
A=[4 -2 -10;2 10 -12;-4 -6 16]; b=[-10 32 -16]'; x= A\b
x =
2.0000
4.0000
1.0000
Ejercicio 3
Para la matriz de coeficientes anterior hallar la factorización LU, es decir A = LU y aplicar a continuación X = U-1L-1B para resolver el sistema anterior.
A=[4 -2 -10;2 10 -12;-4 -6 16]; B=[-10 32 -16]'; [L, U] =lu(A) W=L*U X=inv(U)*inv(L)*B
L =
1.0000 0 0
0.5000 1.0000 0
-1.0000 -0.7273 1.0000
U =
4.0000 -2.0000 -10.0000
0 11.0000 -7.0000
0 0 0.9091
W =
4 -2 -10
2 10 -12
-4 -6 16
X =
2
4
1
Ejercico 4
Hallar los autovalores y autovectores de la matriz A:
A=[0 1 -1;-6 -11 6;-6 -11 5]; [P,D]= eig (A); T1=A*P T2=P*D
T1 = -0.7071 0.4364 0.2762 -0.0000 0.8729 1.6570 -0.7071 1.7457 2.4856 T2 = -0.7071 0.4364 0.2762 -0.0000 0.8729 1.6570 -0.7071 1.7457 2.4856
Ejercicio 5
Para el siguiente circuito, determinar los voltajes de los nodos V1 y V2 y la potencia entregada por cada fuente:
X=[1.5-2j -.35+1.2j; -.35+1.2j 0.9-1.6j];
I=[30+40j;20+15j];
disp('Resultado:')
V=X\I
Potencia_S=V.*conj(I)
Resultado: V = 3.5902 +35.0928i 6.0155 +36.2212i Potencia_S = 1.0e+003 * 1.5114 + 0.9092i 0.6636 + 0.6342i
Ejercicio 6
Escribir una función recursiva para resolver el problema de la Torres de Hanoi y probarla para un valor 5 discos.
hanoi(5,'a','b','c')
mover disco 1 de a a c mover disco 2 de a a b mover disco 1 de c a b mover disco 3 de a a c mover disco 1 de b a a mover disco 2 de b a c mover disco 1 de a a c mover disco 4 de a a b mover disco 1 de c a b mover disco 2 de c a a mover disco 1 de b a a mover disco 3 de c a b mover disco 1 de a a c mover disco 2 de a a b mover disco 1 de c a b mover disco 5 de a a c mover disco 1 de b a a mover disco 2 de b a c mover disco 1 de a a c mover disco 3 de b a a mover disco 1 de c a b mover disco 2 de c a a mover disco 1 de b a a mover disco 4 de b a c mover disco 1 de a a c mover disco 2 de a a b mover disco 1 de c a b mover disco 3 de a a c mover disco 1 de b a a mover disco 2 de b a c mover disco 1 de a a c
Ejercicio 7
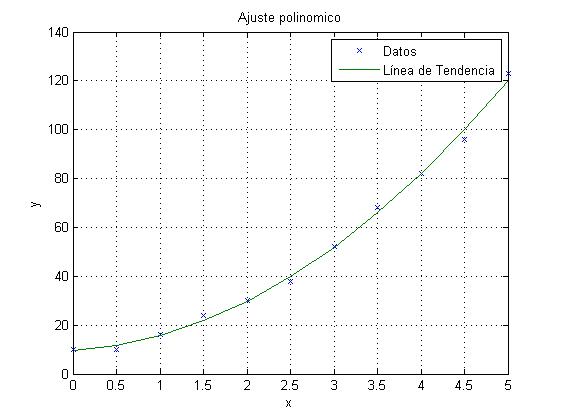
Ajustar un polinomio de orden 2 a los siguientes datos: Datos x: [0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0] Datos y: [10, 10, 16, 24, 30, 38, 52, 68, 82, 96, 123] y graficar los puntos dados con el símbolo x y la curva ajustada con una línea sólida. Colocar una leyenda adecuada, etiquetas en los ejes y un título al gráfico.
x=0:0.5:5; y=[10 10 16 24 30 38 52 68 82 96 123]; p=polyfit(x,y,2) yp=polyval(p,x); plot(x,y,'x',x,yp); xlabel('x'),ylabel('y'),grid,title('Ajuste polinomico') legend('Datos','Línea de Tendencia')
p =
4.0233 2.0107 9.6783
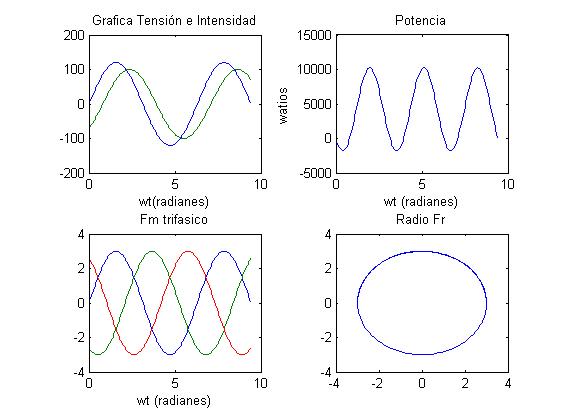
Ejercicio 8
Partir la ventana Figure en cuatro particiones (2x2) y graficar las siguientes funciones para wt de 0 a 3p en pasos de 0.05 Graficar v = 120 seno wt e i = 100 seno(wt - p/4 ) en función de wt en la parte superior izquierda Graficar p = vi en la parte superior izquierda Para Fm = 3.0, graficar fa = Fm seno wt, fb = Fm seno(wt – 2 pi/3) y fc = Fm seno(wt – 4 pi/3) en función de wt en la parte inferior izquierda Para fR = 3.0, construir un círculo de radio fR en la parte inferior derecha
wt=0:0.05:3*pi; v=120*sin(wt); i=100*sin(wt-(pi/4)); subplot(2,2,1) plot(wt,v,wt,i) title('Grafica Tensión e Intensidad'),xlabel('wt(radianes)') p=v.*i; subplot(2,2,2) plot(wt,p) title('Potencia'),xlabel('wt (radianes)'),ylabel('watios') Fm=3.0; Fa=Fm*sin(wt); Fb=Fm*sin(wt-2*pi/3); Fc=Fm*sin(wt-4*pi/3); subplot(2,2,3) plot(wt,Fa,wt,Fb,wt,Fc) title('Fm trifasico'),xlabel('wt (radianes)') subplot(2,2,4) Fr=3.0; plot(-Fr*cos(wt),Fr*sin(wt)) title('Radio Fr')
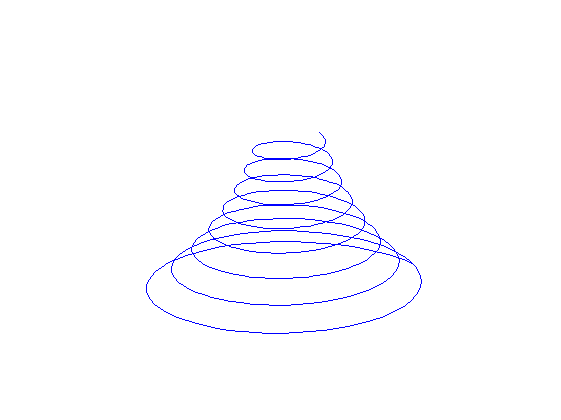
Ejercicio 9
Graficar la curva paramétrica X(t)= Exp(-0.03*t)*Cos(t) Y(t)= Exp(-0.03*t)*Sin(t) Z(t)= t
t=0:0.1:16*pi;
X=exp(-0.03*t).*cos(t);
Y=exp(-0.03*t).*sin(t);
Z=t;
subplot(1,1,1)
plot3(X,Y,Z), axis off
Ejercicio 10
Graficar la curva Z(t)=Sin(x)*cos(y)*Exp(-(x^2+y^2)^0.5) Para un intervalo de -4 a 4 en pasos de 0.3
[x,y]=meshgrid(-4:0.3:4); z=sin(x).*cos(y).*exp(-(x.^2+y.^2).^0.5); mesh(x,y,z)
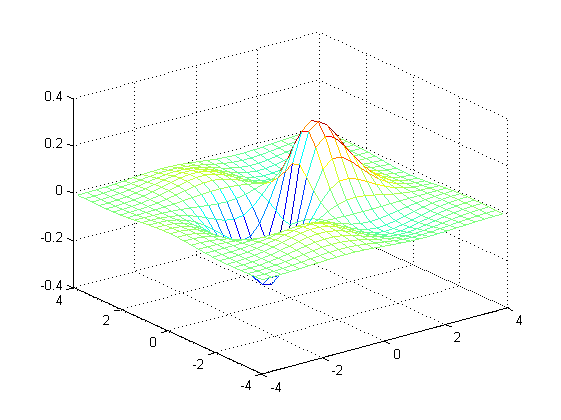
Ejercicio 11
Hallar las raíces del polinomio f(x)= x^4-(35*x^2)+(50*x)+24
poli=[1 0 -35 50 24]; r=roots(poli)
r =
-6.4910
4.8706
2.0000
-0.3796
Ejercicio 12
Resolver la ecuación diferencial d2/dt2(y)+2*d/dt(y)+y=h(t)
Ejemploode [t, yy] = ode45(@HalfSine, [0 35], [1 0], [ ], 0.15); plot(t, yy(:,1))
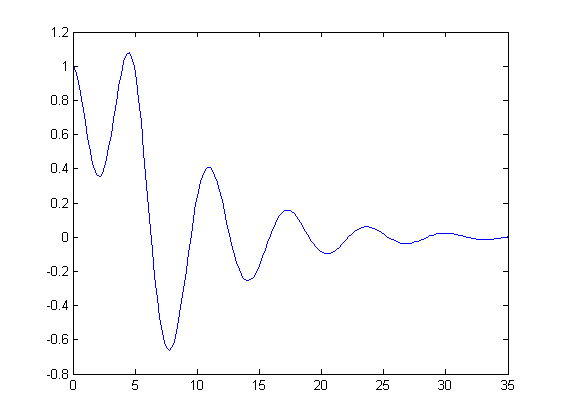
Ejercicio 13
Tomando como base las condiciones del ejemplo de la transformada de Fourier de los apuntes (pág. 124), graficar para las siguientes señales la gráfica de la señal en el tiempo y la gráfica de la amplitud espectral en función de la frecuencia: g(t)= (B0*Sin(2*Pi*f0*t))+(B0/2*sin(2*Pi*2*f0*t)) g(t)= Exp(-2*t)*Sin(2*Pi*f0*t) g(t)= Sin(2*Pi*f0*t+5*Sin(2*Pi*f0*t/10)) g(t)= Sin(2*Pi*f0*t-(5*Exp(-2*t)))
k = 5; m = 10; fo = 10; Bo = 2.5; N = 2^m; T = 2^k/fo; ts = (0:N-1)*T/N; df = (0:N/2-1)/T; SampledSignal = Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*fo*2*ts); An = abs(fft(SampledSignal, N))/N; plot(df, 2*An(1:N/2))
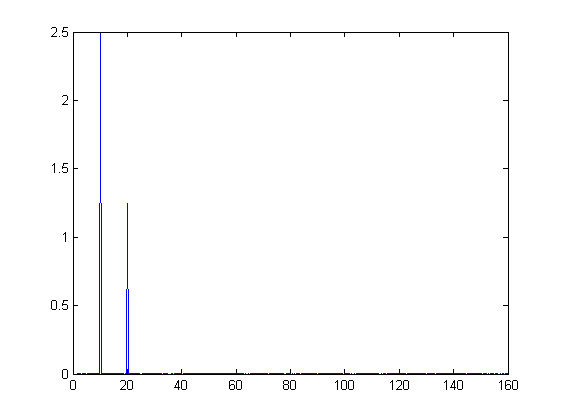
Ejercicio 14
Leer y graficar la imagen WindTunnel.jpg de las transparencias y graficar en sendos gráficos el valor del color rojo de la imagen en función del ancho de la imagen y el histograma del mismo para una fila de la imagen que se pide al usuario. Mostrar el valor para 200
subplot(1,1,1) A = imread('WindTunnel.jpg', 'jpeg'); image(A) hold on figure r= A(200, :, 1); plot(r, 'r');

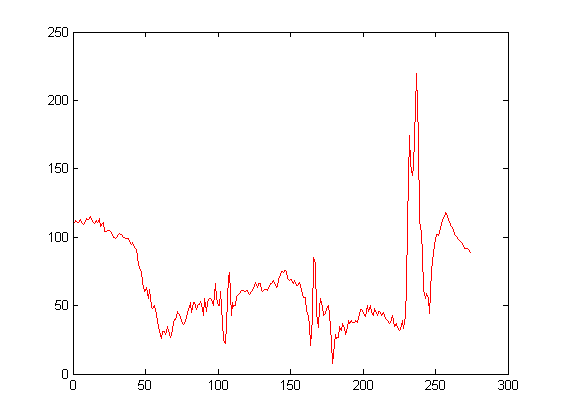
Ejercicio 15
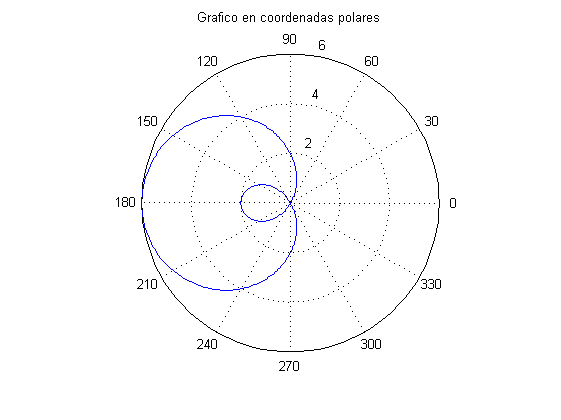
Graficar la función en coordenadas polares :
theta = linspace(-pi, pi, 360);
r= 2 - 4*cos(theta);
figure
polar(theta, r);
title('Grafico en coordenadas polares')